this pretty much sums up my PhD topic. / jól összefoglalja a doktorimat. Bokor Sándor, az Ózdi Munkaügyi Kpt. vezetője. Ózd, 1993 Forrás: index.hu
Szerző: Zoltán Ginelli
Zoltán Ginelli is a geographer and historian of science. His research is in the geographies of knowledge, the history of geography, and global and transnational history. His main focus is on the historical relations between Eastern Europe and the Global South/Third World in the 19th and 20th centuries, including topics such as development and regional planning, (post)colonialism and racism, Cold War foreign policy, and travel writing. He lectured at various universities and colleges, and worked as an assistant researcher in the 1989 After 1989 and Socialism Goes Global projects at the University of Exeter (2015–2019). His current project, Postcolonial Hungary explores Hungarian semiperipheral colonial history from a world-systemic perspective. He is curating the exhibition Transperiphery Movement: Global Eastern Europe and Global South, and finishing his book based on 7 years of research about the global history of the quantitative revolution in geography.
zginelli@gmail.com
A német mindig tárgyilagosságra törekvő és nem felületes
“A német tudományos folyóiratot, könyvet sohasem azzal az előítélettel nyitjuk fel, mint egyik-másik balkáni nép “tudományos” szellemi termékét. A német mindig tárgyilagosságra törekvő és nem felületes, sőt a “német alaposság” közmondásos. Előttünk fekszik egy erdélyi […]
Assembling Hungarian socialist urban and regional planning in the early post-WWII period
This paper explores the early post-WWII era institutionalization of socialist urban and regional planning, and the uneven relations between the nation-state and the urban scale in Hungary. From the perspective of science and technology studies […]
Földrajzi determinizmus Fodor Ferenc gazdasági földrajzában
A Teleki-tanítvány Fodor Ferenc az egyik legjelentősebb magyar geográfus volt a két világháború közötti időszakban. Az 1930-as évekre Teleki nyomán megerősödő új területet, a gazdasági földrajzot tőle tanulta sok-sok diák. Fodor 1933-ban kiadott “Bevezetés a gazdasági földrajzba” című egyetemi tankönyve ezeknek a “természeti törvényeknek” a bemutatásával foglalkozott: az emberi civilizáció fejlődését a természetföldrajzi viszonyok alapvetően meghatározzák. Ezt nevezi a szakirodalom – némileg leegyszerűsítve – “földrajzi determinizmusnak”.
A short summary of my PhD project
My doctoral research project is about the geographies of the so-called ‘quantitative revolution’. I am interested in the circulation of knowledge produced in the emerging global centre(s), to provide a sort of overview of the ways […]
„A területi egyenlőtlenségek csupán a társadalmi egyenlőtlenségek térbeli megjelenési formái.” (Wiener György)
Miről szól a kritikai földrajz?
Miről szól a kritikai földrajz? “Az alkalmazott geográfiának azon formája ellen, amely magát az eladhatóság érdekében „semlegesnek” kiáltja ki, továbbá olyan technikai tudás fontosságát propagálja, melyet – Kenzer (in Johnston, R. J. et al 2000, […]
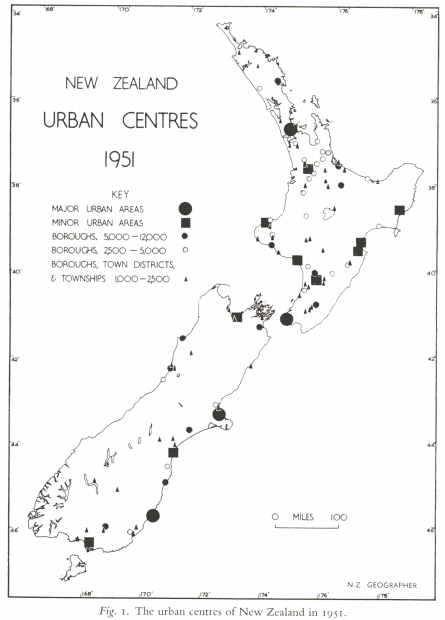
The urban hierarchy of New Zealand in the 1950s
The great Ron J. Johnston wrote an article in 1969 on the development of urban geography in New Zealand after 1945. He writes about a “nomothetic movement” emerging from the 1950s, which drew its sources from the geography of the UK and the US. One of the main figures in New Zealand was L. L. Pownall, who argued already in 1952 for an urban geography building on inductive generalizations.
Zoltán Ginelli 